De Rham invariant

In geometric topology, the de Rham invariant is a mod 2 invariant of a (4k+1)-dimensional manifold, that is, an element of 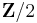$\mathbf{Z}/2$ – either 0 or 1. It can be thought of as the simply-connected symmetric L-group 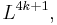$L^{4k%2B1},$ and thus analogous to the other invariants from L-theory: the signature, a 4k-dimensional invariant, and the Kervaire invariant, a (4k+2)-dimensional invariant.

It is named for Swiss mathematician Georges de Rham, and used in surgery theory.^[1]^[2]

Definition

The de Rham invariant of a (4k+1)-dimensional manifold can be defined in various equivalent ways:^[3]

the rank of the 2-torsion in 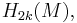$H_{2k}(M),$ as an integer mod 2;
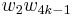the Stiefel–Whitney number $w_2w_{4k-1}$ ;
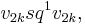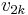the (squared) Wu number, $v_{2k}sq^1v_{2k},$ where $v_{2k}$ is the Wu class and 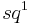$sq^1$ is the Steenrod square; formally, as with all characteristic numbers, this is evaluated on the fundamental class: $(v_{2k}sq^1v_{2k}(M),[M])$ ;
in terms of a semicharacteristic.

References

^ Morgan & Sullivan, The transversality characteristic class and linking cycles in surgery theory, 1974
^ John W. Morgan, A product formula for surgery obstructions, 1978
^ (Lusztig, Milnor & Peterson 1969)

Lusztig, G.; Milnor, J.; Peterson, F. P. (1969), "Semi-characteristics and cobordism", Topology 8: 357–360
Chess, Daniel, A Poincaré-Hopf type theorem for the de Rham invariant, 1980